Dentre as 7 ferramentas da qualidade, a carta de controle é sem dúvida a mais utilizada nas empresas e indústrias. Nenhuma outra ferramenta capta melhor as informações de um processo como esta. A carta de controle é utilizada para determinar se o processo está operando em controle estatístico e basicamente é representada por um gráfico em execução que inclui estatisticamente limites de controle superior e inferior. Neste artigo, será apresentado como as cartas de controle podem contribuir para aperfeiçoar o processo de fabricação e assim aumentar a competitividade da sua empresa.
1 – O que é e para que serve a carta de controle?
O objetivo de uma carta de controle é detectar quaisquer alterações indesejadas em um processo, sendo que quando ocorrerem mudanças, estas serão sinalizadas por pontos anormais em um gráfico.
Para obter informações de um processo, primeiramente é necessário entender os conceitos de população e amostras, que podem ser definidos da seguinte forma:
- População: lote de produtos/serviços ou período de tempo que se quer analisar.
- Amostra: quantidade de valores observados pertencentes ou representativos de uma população.

Figura 2 – Cartas de Controle – Amostra estatística de controle da população
Na Figura acima é possível observar bem a definição de população e amostra. Quando é desejado mensurar as características de uma determinada população, podemos fazê-la medindo as características de cada indivíduo que compõe esta população e com base nas informações obtidas, entender como ela é delineada. No entanto, na maioria das vezes, a população é muito grande e medir cada indivíduo que a compõe torna-se oneroso e em alguns casos praticamente impossível. Imagine por exemplo entrevistar todos os 140 milhões de eleitores brasileiros para sabermos quem será o novo ganhador de uma disputa pela presidência. Por este motivo, surgiram ferramentas, como a estatística, que são capazes de tratar informações coletadas de amostragens e subsidiar conclusões sobre uma população com uma precisão tão próxima quanto se fossem estudados cada indivíduo da população.
A partir dos conceitos acima, foi possível aplicar a ferramenta estatística na indústria, com o objetivo de estudar melhor os produtos e ocorrências de não conformidades nos processos de fabricação. E ainda, o criador das cartas de controle, Dr. Shewhart, demonstrou que se fossem definidos limites superiores e inferiores a três vezes o desvio padrão (mais e menos, respectivamente) de uma quantidade de amostras, estaríamos garantindo que 99,73% da variação de causas comuns cairiam dentro desses limites estabelecendo então a definição de controle no processo. Pode-se dizer portanto que um processo está em controle estatístico quando as medições do processo variarem aleatoriamente dentro dos limites de controle.
Importante ressaltar que os limites superiores e inferiores não são o mesmo que tolerância ou limite de especificação. Nas suas definições, limites de controle são uma função da forma de como o processo realmente se comporta ao longo do tempo. Por outro lado, limites de especificação ou tolerância são uma função que diz respeito ao projeto do processo para que ele desempenhe algo e não necessariamente tem qualquer relação direta com o desempenho real do mesmo.
2 – Como utilizar a carta de controle
Primeiro, é importante determinar o que será controlado (diâmetro de um cilindro, altura de uma haste, etc.). Após isto, é necessário definir o tamanho da amostra que será coletada e de quanto em quanto tempo serão realizadas as amostragens (1 hora, 1 dia, 1 semana, etc). Por último, basta definir o limite superior e o limite inferior da carta controle.
a) Escolha do tipo de carta
Devemos determinar qual o tipo de carta de controle deverá ser utilizada. As cartas de controle podem conter dois tipos de dados: dados variáveis ou dados tipo atributos. Em geral, se for desejado utilizar dados variáveis, é necessário adotar medidas em unidades, tais como comprimento, temperatura, etc. Por outro lado, os dados do tipo atributos exigem uma decisão: “passa/não passa”, “aceitável/não aceitável”, “conforme/não conforme”, “sucesso/insucesso”.
Caso os dados forem do tipo atributo, é necessário ainda decidir se os dados são defeitos ou defeituosos. Basicamente o defeito é um subconjunto de defeituoso. Um defeito não significa necessariamente que o produto ou serviço seja defeituoso. A título de exemplo, vamos considerar uma haste cilíndrica como um produto final. Os defeitos possíveis são: quebra, dureza, tolerância dimensional, etc. Neste caso, uma haste defeituosa poderá ter um ou mais defeitos e o fato da haste conter defeitos não necessariamente caracteriza ela como defeituosa, pois o produto será considerado defeituoso somente quando ele possuir defeitos que não são tolerados pelo cliente.
Com os conceitos claros, podemos utilizar o fluxograma abaixo para definir a carta de controle mais adequada para cada situação.
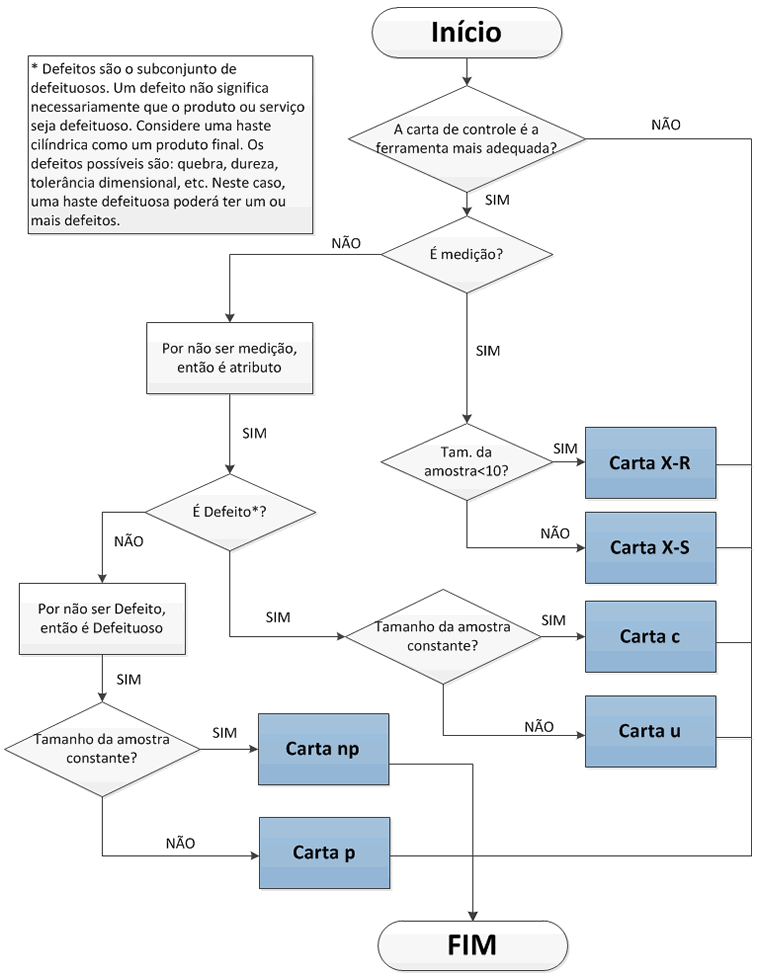
Figura 3 – Fluxograma decisão carta de controle estatístico de processo
b) Construção da Carta de Controle
Neste artigo iremos construir 2 tipos de cartas, ambas por variáveis para exemplificar como funcionam. Para a construção das cartas de controle por variáveis, a análise deve ser feita aos pares, observando a centralização e a dispersão. Sendo assim, dois gráficos são construídos para cada tipo:
- Gráfico de média e o de desvio padrão (X – S)
- Gráfico de média e o de amplitude (X – R)
Abaixo na figura pode ser observado um resumo passo a passo de como construir uma carta de controle.

Figura 4 – Fórmulas aplicáveis à carta de controle por variável.
Os passos para a construção podem ser descritos da seguinte forma:
1 – Coleta dos dados: Nesta etapa são definidos o tamanho adotado para as amostras, que deverá ser constante, bem como a quantidade de amostras e a frequência de amostragem. A frequência de amostragem dependerá da quantidade de produtos defeituosos. Se houver bastante incidência de produtos defeituosos, a frequência deverá ser maior (de hora em hora, etc.). Por outro lado, se forem poucos defeituosos, a frequência poderá ser menor, com intervalos maiores. Costuma-se adotar também uma relação entre a quantidade de amostras (k) com o tamanho da amostra (n), sendo k*n > 100.
2 – Cálculo das médias das amostras. A título de exemplo, vamos pegar uma quantidade pequena de amostras para demonstrar como fazer este cálculo. Ex.: Supondo uma medição do diâmetro de uma haste em 1 dia, onde tem-se 6 amostras, contendo 5 itens, coletadas de 4 em 4 horas, temos: A1 (32,30,31,34,32), A2 (30,33,32,31,31), A3 (34,32,31,33,30), A4 (29,33,32,30,31), A5 (30,33,29,31,33), A6 (33,30,32,31,30). A média da primeira amostragem será: X1 = (32+30+31+34+32)/5 = 31.8. Portanto teremos: X1=31.8, X2=31.4, X3=32, X4=31, X5=31.2 e X6=31.2.
3 – Cálculo da média do processo. Para o nosso exemplo, esta média será: X = (X1 + X2 + X3 + X4 + X5 + X6)/6 = 31.43.
4 – A partir da quarta etapa, os tipos de carta já se diferenciam, partindo para o cálculo do desvio padrão de cada item da amostra (X-S) ou amplitude (X-R). No nosso exemplo, o tamanho da amostra (n) = 5. Sendo assim, o ideal seria utilizar a carta de amplitude (X-R), porém vamos obter as duas cartas para exemplificar as diferenças entre um e outro.
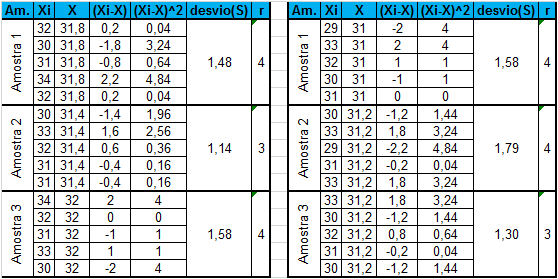
Figura 5 – Tabela com os Desvios Padrão e Amplitude
5 – Agora, com os valores obtidos para cada amostra, o desvio padrão médio e a amplitude média deverão ser calculados. Utilizando as fórmula do item 5 da Figura x, tem-se: s=(1,48+1,14+1,58+1,82+1,91+1,47)/6 = 1,56 e r=(4+3+4+4+4+3)/6=3,66.
6 – No sexto passo, vamos obter os limites de controle para as cartas de média. A partir daqui é necessário utilizar uma tabela contendo as constantes (A2, A3, B3, B4, D3, D4), conforme Figura abaixo:

Figura 6 – Tabela com constantes aplicáveis nas fórmulas da Figura 4
Com a tabela de constantes e as fórmulas descritas no passo 6 da Figura 4, podemos obter os valores para média utilizando a tabela da Figura 6. Teremos então:
- Média (X-S) LSC=31,43+1,427*1,56=33,656; LIC=31,43-1,427*1,56=29,20;
- Média (X-R) LSC=31,43+0,577*3,66=33,542; LIC=31,43-0,577*3,66=29,32;
7 – No sétimo passo, finalmente serão calculados os limites de controle para as cartas de desvio padrão e amplitude:
- Desvio Padrão (X-S) LSC=2,089*1,56 = 3,259; LIC=0*1,56=0;
- Amplitude (X-R) LSC=3,66*2,114 = 7,737; LIC=3,66*0=0;
8 – Finalmente, agora é necessário desenhar os gráficos.

Figura 7 – Gráficos obtidos para média, desvio-padrão e amplitude.
c) Identificação e eliminação de quaisquer causas especiais ou atribuíveis de variação
Para determinar se existem causas de variação em um processo utilizando a carta de controle, é muito importante observar sete “sinais” ou regras básicas que demonstram variabilidade neste processo. A probabilidade de alguns destes sete eventos ocorrerem aleatoriamente é muito pequena. Este é o motivo pelo qual estes sinais indicam alguma mudança no processo.
As sete regras são:
- Um ou mais pontos fora dos limites de controle;
- Sete ou mais pontos consecutivos acima ou abaixo da linha central
- Seis pontos consecutivos em linha ascendente ou descendente continuamente;
- Quatorze pontos consecutivos alternando acima e abaixo;
- Três pontos consecutivos sendo 2 deles do mesmo lado em relação a linha central e fora de 2/3 em relação à linha central;
- Quinze ou mais pontos consecutivos contidos em um intervalo de 1/3 em relação à média;
- 8 pontos em ambos os lados da região central com nenhum deles dentro do limite de 1/3 em relação à linha central
Elas podem ser visualizadas na figura abaixo:
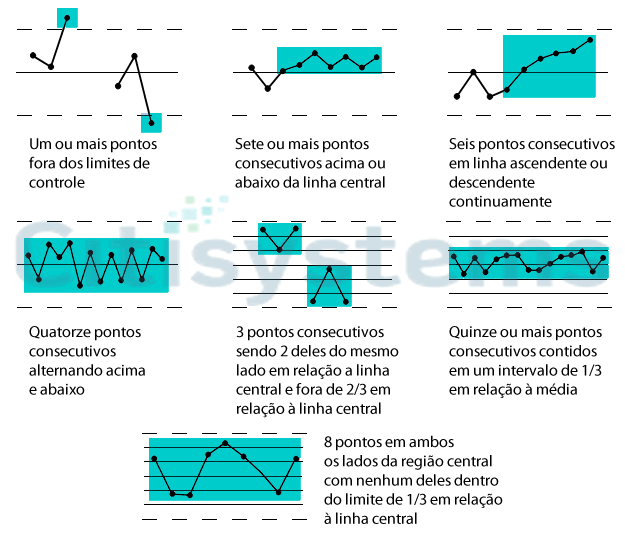
Figura 8 – Regras aplicadas ao Controle Estatistico de Processo
d) Redução da variabilidade global
Após eliminar todas as causas especiais, é importante trabalhar no sentido de reduzir as variabilidades que restam no processo. Isto requer, usualmente, mudanças fundamentais no processo, sendo que estas mudanças, na maioria das vezes requerem uma assistência gerencial. Para atingir um processo de melhoria contínua, é essencial reduzir a variabilidade.
3 – Vantagem de utilizar a carta de controle
- Conhecer as causas raízes dos problemas ocorridos no processo;
- Registro formal das ocorrências, podendo ser utilizado como histórico posterior;
- Registra o esforço aplicado pela equipe para controlar o processo;
- As cartas de controle colaboram para aperfeiçoar o processo;
- Fornece aos operadores um controle para o processo;
- Melhoria na qualidade, custo por unidade e eficiência.
Um ponto importante que deve ser observado é com relação a utilização cada vez mais frequente de softwares para controle estatístico de processo na indústria (saiba mais sobre estes softwares clicando aqui). Estes sistemas possibilitam agilidade na realização de análises e tomada de decisões fornecendo um alto nível de qualidade nos processos. Facilitam ainda a coleta e análise das informações, que podem ser realizadas em um sistema centralizado. Por isto é sempre importante analisar a possibilidade da automatização e os ganhos que poderão ser alcançados com tais ferramentas.
Está gostando desse artigo?
Cadastre-se hoje e receba atualizações por e-mail. Respeitamos a sua privacidade e você nunca terá seu e-mail divulgado.

![5W2H: Saiba Designar Tarefas [Exemplo Prático]](https://www.citisystems.com.br/wp-content/uploads/2016/08/5w2h-500x383.png)



